Question

Given the following sets, find the set A’ n (B U C ‘)

Answer 1

`A^(\prime)\cap(B\cup C^(\prime))=\lbrace1,7,8,9,10\rbrace`

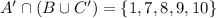
Explanations:

Given the following sets of numbers:

`\begin{gathered} U=\mleft\lbrace1,2,3,\ldots10\mright\rbrace \\ A=\mleft\lbrace2,\text{ 3, 4, 6}\mright\rbrace \\ B=\mleft\lbrace1,\text{ 3, 8}\mright\rbrace \\ C=\mleft\lbrace1,\text{ 3, 4, 5, 8}\mright\rbrace \end{gathered}`

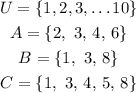
Before we get the required set, we will need to get the complement of set A (A') and the complement of set C'.

Compliments of a set are the elements in the universal set but not in the original set.

The complements of A and C are given as:

`\begin{gathered} A^(\prime)=\mleft\lbrace1,5,7,8,9,10\mright\rbrace \\ C^(\prime)=\mleft\lbrace2,\text{ 6, 7, }9,\text{ 10}\mright\rbrace \end{gathered}`

For the element of the set A' n (B U C')

First, we need to get (BUC')

`B\cup C^(\prime)=\mleft\lbrace1,2,3,6,7,8,9,10\mright\rbrace`

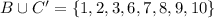
Note that the union of two sets (U) is the combination of all the elements in both sets without repeating elements.

`A^(\prime)\cap(B\cup C^(\prime))=\mleft\lbrace1,7,8,9,10\mright\rbrace`

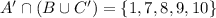
Note that the intersection of two sets (n) are the common elements in both given sets.