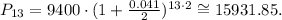To solve this problem we will use the formula for compound interest:
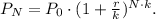
Where:
• P_N, is the balance in the account after N years,
,
• P_0, is the starting balance of the account (also called an initial deposit, or principal),
,
• r, is the annual interest rate in decimal form,
,
• k, is the number of compounding periods in one year.
In this problem we have that:
• N = 13 (13 years),
,
• P_N is the unknown,
,
• P_0 = $9400,
,
• r = 4.1/100 = 0.041,
,
• k = 2 (because the interest compounded twice per year).
Replacing these values in the formula above, we find:
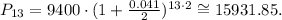
Answer