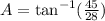Question

Write a trig equation to be used to find the measure of angle A?

Answer 1

Given the triangle ABC as shown below:

To evaluate angle A,

Step 1: Identify the sides of the triangle ABC.

Thus, using A as the angle of focus,

`\begin{gathered} AB\implies\text{hypotenuse} \\ AC\implies\text{Adjacent} \\ BC\implies\text{Opposite} \end{gathered}`

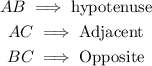
Step 2: Write a trigonometric equation to measure A

Using trigonometric ratio,

`\begin{gathered} \tan \text{ A= }(opposite)/(Adjacent) \\ =(BC)/(AC) \\ \text{where BC=45, AC=28} \\ \text{thus,} \\ \tan \text{ A=}(45)/(28) \\ \Rightarrow A=\tan ^(-1)((45)/(28)) \end{gathered}`

Hence, the trigonometric equation is

`A=\tan ^(-1)((45)/(28))`