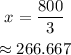Use the properties of equalities to solve for x:
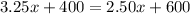
We would like the terms which include the variable x to be on one single side of the equation, and the other terms on the other side. So, substract 2.50x from both sides:
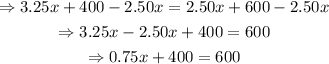
Next, substract 400 from both sides:
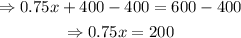
Divide both sides by 0.75:
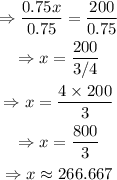
Therefore: