Answer:
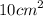
Explanation:
Given,
Sum of parallel sides of the trapezium = 10 cm
Distance between or Height of the trapezium = 2 cm
As we know,
Area of a trapezium
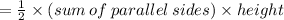
Therefore,
Area of the given trapezium will be,
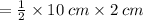
= 1 × 10 cm × 1 cm
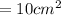
Hence,
The Area of the trapezium is 10 sq.cm (Ans)