Question

8. There are approximately 2.2046 kilograms in 1 pound. There are about 0.4536 pounds in 1 kilogram. To convert 112 lbs to kilograms, which conversion factor should be used? Why? I

Answer 1

Notice that 1 lb is equivalent to 0.45 kilograms, so the conversion factor would be:

`(\frac{0.453592\text{ kg}}{1\text{ lb}})`

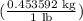
thus, to convert 112 lbs to kilograms we can do the following expression:

`\text{ 112 lb }(\frac{0.453592\text{ kg}}{1\text{ lb}})\text{ = }50.\text{ }80\text{ lb}`

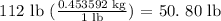
we can conclude that the correct answer is:

the conversion factor to convert 112 lbs to kilograms is

`(\frac{0.453592\text{ kg}}{1\text{ lb}})`

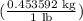
Note that this is the conversion factor because this is an equivalence between the two given amounts.