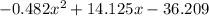Given a quadratic equation: y = ax² + bx + c, "a", "b" and "c" are the coefficients of the regression and can be estimated using the formulas below.
a = {[Σ x²y * Σ xx ] - [Σ xy * Σ xx² ] } / { [ Σ xx * Σ x²x²] - [Σ xx² ]²}
b = {[Σ xy * Σ x²x² ] - [Σ x²y * Σ xx² ] } / { [ Σ xx * Σ x²x²] - [Σ xx² ]²}
c = [Σ y / n ] - { b * [ Σ x / n ] } - { a * [ Σ x² / n ]}
Where:
Σ xx = [Σ x²] - [ ( Σ x )² / n]
Σ xy = [Σ x y] - [ ( Σ x * Σ y ) / n]
Σ xx² = [Σ x³] - [ ( Σ x² * Σ x ) / n]
Σ x²y = [Σ x²y] - [ ( Σ x² * Σ y ) / n]
Σ x²x² = [Σ x⁴] - [ ( Σ x² )² / n]
And:
x and y are the Variables.
n = Number of Values or Elements
Σ x = Sum of x Scores
Σ y = Sum of y Scores
Σ x² = Sum of Square of x
Σ x³ = Sum of Cube of x
Σ x⁴ = Sum of Power Four of x
Σ xy= Sum of the Product of x and y
Σ x²y = Sum of Square of x and y
To solve the problem, follow the steps below.
Step 01: Find n and the values of x and y.
n = 6.
x = 8, 10, 12, 14, 16, 18
y = 45.94, 56.84, 63.88, 67.07, 66.4, 61.87
Step 02: Find Σ x, Σ y, Σ x², Σx³, Σ x⁴, Σ xy, Σ x²y
* (,) represents a decimal point.
Step 03: Find Σ xx, Σ xy, Σ xx², Σ x²y, Σ x²x²
Substitute the values above in the equations for each variable:
Σ xx = [Σ x²] - [ ( Σ x )² / n]
Σ xy = [Σ x y] - [ ( Σ x * Σ y ) / n]
Σ xx² = [Σ x³] - [ ( Σ x² * Σ x ) / n]
Σ x²y = [Σ x²y] - [ ( Σ x² * Σ y ) / n]
Σ x²x² = [Σ x⁴] - [ ( Σ x² )² / n]
![\begin{gathered} \sum_^xx=\operatorname{\sum}_^x^2-\frac{(\operatorname{\sum}_^x)^2}{n} \\ \sum_^xx=1084-(78^2)/(6) \\ \sum_^xx=1084-(6084)/(6) \\ \sum_^xx=1084-1014 \\ \sum_^xx=70 \end{gathered}]()
Doing the same for the other variables, you have the results:
* (,) represents a decimal point.
Step 03: Find "a".
a = {[Σ x²y * Σ xx ] - [Σ xy * Σ xx² ] } / { [ Σ xx * Σ x²x²] - [Σ xx² ]²}
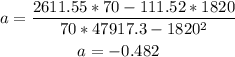
Step 04: Find "b".
b = {[Σ xy * Σ x²x² ] - [Σ x²y * Σ xx² ] } / { [ Σ xx * Σ x²x²] - [Σ xx² ]²}
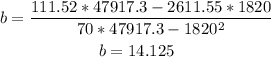
Step 05: Find "c".
c = [Σ y / n ] - { b * [ Σ x / n ] } - { a * [ Σ x² / n ]}
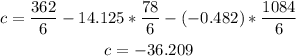
Answer:
The equation is: