anGiven the infinite series:
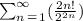
You need to remember that, by definition, given an infinite series:
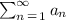
(a) The formula for applying the Ratio Test is:
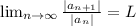
By definition:
1. If:
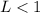
The series converges.
2. If:
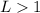
Or:
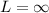
The series diverges.
3. If:
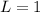
The Ratio Test is inconclusive.
Therefore, you need to set up:
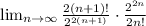
Simplifying, you get:
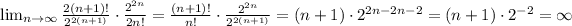
(b) Notice that:
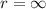
Therefore, this indicates that the series diverges.
Hence, the answers are:
(a)
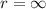
(b) It tells that the series diverges.