Question

Find the 19th term of an arithmetic sequence if the first term is 24 and the common difference is 1/2Round your answer to 2 decimal places as needed..

Answer 1

33.00

Step-by-step explanation:

We are given the following information:

This is an arithmetic sequence

The first term is 24

The common difference is 1/2

The formula for an arithmetic sequence is given by:

`\begin{gathered} a_n=a+(n-1)d \\ a=24 \\ d=(1)/(2) \\ \text{For the 19th term,} \\ n=19 \\ \text{Substitute these values into the formula, we have:} \\ a_(19)=24+(19-1)\cdot(1)/(2) \\ a_(19)=24+18((1)/(2)) \\ a_(19)=24+9 \\ a_(19)=33=33.00 \\ \\ \therefore a_(19)=33.00 \end{gathered}`

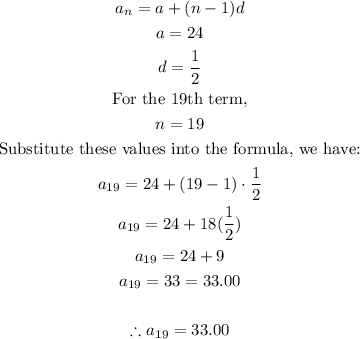
Therefore, the 19th term in the sequence is 33.00