Question

A rock group is playing in a bar. Sound emerging from the door spreads uniformly in all directions. The intensity level of the music is 92 dB at a distance of 3.52 m from the door. At what distance is the music just barely audible to a person with a normal threshold of hearing

Answer 1

The decibel scale is given by:

`dB=10\log _(10)((I)/(I_0))`

where I is the sound intensity and I0 is the threshold intensity; plugging the value given for the music level we have that:

`\begin{gathered} 92=10\log _(10)((I)/(1*10^(-12))) \\ \log _(10)((I)/(1*10^(-12)))=(92)/(10) \\ (I)/(1*10^(-12))=10^{(92)/(10)} \\ I=1*10^(-12)\cdot10^{(92)/(10)} \\ I=1.58*10^(-3) \end{gathered}`

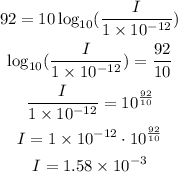
We know that sound intensity is inversely proportional to the square of the distance of the source, then we have:

`(I_1)/(I_2)=(r^2_2)/(r^2_1)`

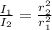
Plugging the values we found:

`\begin{gathered} (1.58*10^(-3))/(1*10^(-12))=(r^2_2)/((3.52)^2) \\ r^2_2=(3.52)^2((1.58*10^(-3))/(1*10^(-12))) \\ r_2=\sqrt[]{(3.52)^2((1.58*10^(-3))/(1*10^(-12)))} \\ r_2=139917 \end{gathered}`

Therefore, the distance is 139917 m. (This is a large distance since sound is not being absorbed)