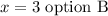Step 1
Given;
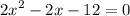
Required; To find the value of x
Step 2
Factorize the equation.
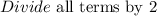
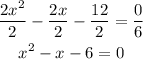
Factors required to factorize the problem are -3x and 2x. We will now replace -x with these factors. That is -x=(-3x+2x)
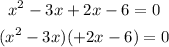
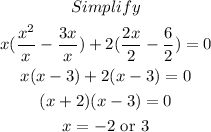
Hence, based on the options, the value of which is a solution to the equation is;
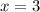
Answer;