Question

There is a lake without any trout in it. The local government, in order to stimulate recreational tourism, transplants 300 trout into the lake. In 2 years, there are 420 trout. How many trout will be there in 7 years assuming nothing changes.

Answer 1

Given an exponential function

`\begin{gathered} y=ab^x \\ a\Rightarrow is\text{ the initial value} \\ b\Rightarrow the\text{ rate} \\ x\Rightarrow\text{time in years} \\ y\Rightarrow nu\text{mber of trout} \end{gathered}`

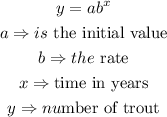
At zero year, the local government transplant 300 trouts, this implies

`\begin{gathered} a=300 \\ x=0 \\ y=300* b^0=300 \end{gathered}`

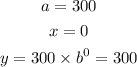
Thus, after 2 years, the trouts grow to 420, we can use this to calculate the rate. This can be shown below;

`\begin{gathered} y=420 \\ x=2 \\ a=300 \\ y=ab^x \\ 420=300(b^2) \\ b^2=(420)/(300) \\ b^2=1.4^{} \\ b=(1.4)^{(1)/(2)} \end{gathered}`

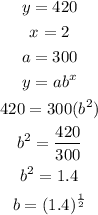
For 7 years the number trouts will be;

`\begin{gathered} y=\text{?} \\ a=300 \\ b=(1.4)^{(1)/(2)} \\ x=7 \\ \text{Given that,} \\ y=300(1.4)^{(x)/(2)} \\ \text{For 7 years} \\ y=300(1.4)^{(7)/(2)} \end{gathered}`
`\begin{gathered} y=300*3.246744585 \\ y=974.0233755\approx974 \end{gathered}`

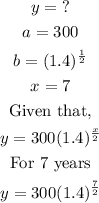
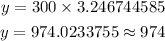
Hence, the number of trout for 7 years is approximately 974 trouts