Question

The average production cost for major movies is 66 million dollars and the standard deviation is 22 million dollars. Assume the production cost distribution is normal. Suppose that 38 randomly selected major movies are researched. Answer the following questions. Give your answers in millions of dollars, not dollars. Round all answers to 4 decimal places where possible.What is the distribution of X ? X ~ N(66,22)What is the distribution of ¯x ? ¯x ~ N(,)For a single randomly selected movie, find the probability that this movie's production cost is between 62 and 66 million dollars. For the group of 38 movies, find the probability that the average production cost is between 62 and 66 million dollars. For part d), is the assumption of normal necessary? Yes No

Answer 1

From the question below

(b) What is the distribution of the mean. This is

`\begin{gathered} \bar{x}\approx N(66,(22)/(√(38))) \\ \bar{x}=N(66,3.5689) \end{gathered}`

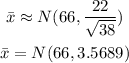
Hence the answer is

N(66, 3.5689) to 4 decimal places

(c) Probability between 62 and 66 million?

We find the Z for both 62 and 22.

For 62 we have

`Z_(62)=(62-66)/(22)=-0.1818181818`

For 66, we have

`Z_(66)=(66-66)/(22)=0`

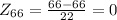
The probability, using Zscore calculator, we have

`P(Z<strong>Hence the answer becomes 0.0721 to 4 decimal places </strong><p></p><p>(d) For here, </p><p>Z for 62 becomes </p>[tex]\begin{gathered} Z_(62)=(62-66)/((22)/(√(38))) \\ =-(4)/((22)/(√(38))) \\ =-1.1208025 \end{gathered}`

Z for 66 becomes

`\begin{gathered} Z_(66)=(66-66)/((22)/(√(38))) \\ =(0)/((22)/(√(38)))=0 \end{gathered}`

The probability using a Zscore calculator becomes

[tex]P(ZHence the answer is 0.3688 to 4 decimal places

(e) The answer is