The given equation is:
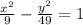
The equation matches the general equation of a hyperbola given by:
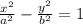
Hence a=3 and b=7.
The center is at origin (0,0)
The vertices are at (3,0) and (-3,0)
The focii are:
![(\sqrt[]{58},0),(-\sqrt[]{58},0)](https://img.qammunity.org/2023/formulas/mathematics/college/3t2nsvs2fiwk4zpfpyu0y0gel18jei85ho.png)
The equation of the asymptotes are:
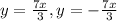
There are no covertices since the hyperbola does not have covertices.
The graph is given below: