Question

Jane has a pre-paid cell phone with Splint. She can't remember the exact costs, but her plan has a monthly fee and a charge for each minute of calling time. In June she used 280 minutes and the cost was $60.00. In July she used 630 minutes and the cost was $95.00.

Answer 1

Part 1:

The Cost function C(x) can be expressed as a linear function y = mx + b, where m is the slope, and b is the y-intercept.

Let x be the number of minutes of calling time, y be the cost for the month.

Given (x,y)

(280,60) → 280 minutes of calling time, with a cost of $60

(630,95) → 630 minutes of calling time, with a cost of $95

First find the slope of the function C(x)

`\begin{gathered} \text{The slope is determined by} \\ m=(y_2-y_1)/(x_2-x_1) \\ \text{If }_{}(x_1,y_1)=\mleft(280,60\mright),\text{ and }(x_2,y_2)=\mleft(630,95\mright)\text{ then the slope is} \\ \\ m=(y_2-y_1)/(x_2-x_1) \\ m=(95-60)/(630-280) \\ m=(35)/(350) \\ m=(1)/(10) \end{gathered}`

Now that we have the slope of the Cost function, we can now solve for its y-intercept. We will use the point (280,60) to solve, but using (630,95) will work just as well.

`\begin{gathered} y=mx+b \\ \text{IF }(x,y)=(280,60)\text{ and }m=(1)/(10),\text{ THEN} \\ \\ y=mx+b \\ 60=((1)/(10))(280)+b \\ 60=(280)/(10)+b \\ 60=28+b \\ 60-28=b \\ 32=b \\ b=32 \end{gathered}`

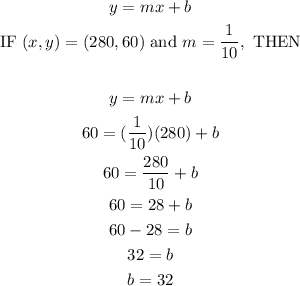
Putting it together the cost function is

`C(x)=(1)/(10)x+32`

Part 2:

If jane used 710 minutes of calling time, how much was her bill.

Substitute x = 710 to the cost function and we get

`\begin{gathered} C(x)=(1)/(10)x+32 \\ C(x)=(1)/(10)(710)+32 \\ C(x)=(710)/(10)+32 \\ C(x)=71+32 \\ C(x)=103 \end{gathered}`

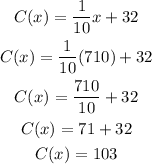
Therefore, her bill for the month of August is $103.