Question

Use the vertex ( h, k ) and a point on the graph ( x, y ) to find the standard form of the equation of the quadratic function:Vertex = (-1,9)Point = (-5,4)G( x )= Answer for coordinate 1 (x- Answer for coordinate 2 )^2 +Answer for coordinate 3

Answer 1

A parabola written in vertex form is

`f(x)=a(x-h)^2+k`

The coordinates (h, k) represents the vertex.

Since the vertex of our problem is (-1, 9), our parabola equation will have the form

`G(x)=a(x-(-1))^2+9=a(x+1)^2+9`

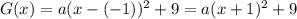
We know that the point (-5, 4) belongs to this parabola. If we evaluate this point on our equation we can determinate the coefficient a.

`\begin{gathered} 4=a(-5+1)^2+9 \\ 4-9=a(-4)^2+9-9 \\ -5=16a \\ 16a=-5 \\ a=-(5)/(16) \end{gathered}`

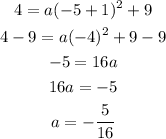
Then, our equation is

`G(x)=-(5)/(16)(x-(-1))^2+9`