Question

If triangle VWX, the measure of angle X=90°, the measure of angle is W=31°, and XV = 8.4 feet. Find the length of WX to the nearest tenth of a foot.

Answer 1

To find the measure of a side in a right triangle as given (have a angle of 90º) you use the trigonometric function. Use the value of the angle W=31º

`\tan \alpha=(opposite)/(adjacent)`

The opposite side of angle W is XV and the adjacent side is y:

`tan31=(8.4ft)/(y)`

Use this equation to find the value of side WX (y):

`\begin{gathered} y\cdot\tan 31=8.4ft \\ y=(8.4ft)/(\tan 31) \\ \\ y=13.979ft \end{gathered}`

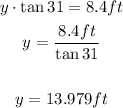
Then, side WX is 14.0 ft (rounded to the nearest tenth)