Question

An x-ray beam (85.97 MeV) strikes a proton at rest and scatters the x-rays through an angle of 100°. What is the wavelength, in pico-meters, of the scattered x-rays?

Answer 1

`466,000\text{ pm}`

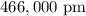
Step-by-step explanation

Parameters given:

Energy of X-ray beam = 85.97 MeV

Scattering angle, θ = 100°

To find the wavelength of the x-ray beam, we have to apply the Compton Effect formula:

`\lambda^(\prime)-\lambda=(h)/(m_0c)[1-\cos\theta]`

where λ' = wavelength of the scattered x-ray

λ = wavelength of the incident x-ray

h = Planck's constant

moc = 1.67 * 10^(-27)

First, we have to find the wavelength of the incident x-ray. To do this, apply the formula for energy:

`\begin{gathered} E=(hc)/(\lambda) \\ \\ \lambda=(hc)/(E) \end{gathered}`

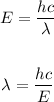
Therefore, the wavelength of the incident x-ray is:

`\begin{gathered} \lambda=(6.626*10^(-34)*3*10^8)/(85.97*10^6*1.6*10^(-19)) \\ \\ \lambda=1.45*10^(-14)\text{ m} \end{gathered}`

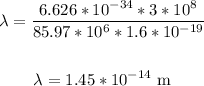
Now, substitute the given and obtained values into the equation for Compton's effect and solve for λ':

`\begin{gathered} λ^(\prime)-1.45*10^(-14)=(6.626*10^(-34))/(1.67*10^(-27))*(1-\cos100) \\ \\ λ^(\prime)-1.45*10^(-14)=(6.626*10^(-34))/(1.67*10^(-27))*1.174 \\ \\ λ^(\prime)-1.45*10^(-14)=4.66*10^(-7) \\ \\ λ^(\prime)=4.66*10^(-7)+1.45*10^(-14) \\ \\ λ^(\prime)=4.66*10^(-7)\text{ m}=466,000\text{ pm} \end{gathered}`

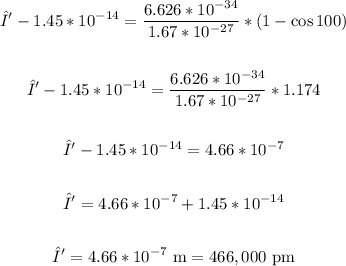
That is the wavelength of the scattered x-rays.