Question

Which image shows a translation of the brown quadrilateral pqrs one unit to the right and four units up?

Answer 1

In order to translate the quadrilateral 1 unit to the right and 4 units up, we just need to sum 1 to the x-coordinate of its points and sum 4 to the y-coordinate of its points.

But also we can already see in the image the options where the new quadrilateral p'q'r's' is above and to the right of the original quadrilateral, as we know that the translation is to the right and upwards.

In the first option, the new quadrilateral is to the left and above the original quadrilateral.

In the second option, the new quadrilateral is to the right and above the original quadrilateral.

In the third option, the new quadrilateral is to the right and below the original quadrilateral.

So the correct option should be the second one.

To confirm that, we can check the coordinate of the points. We have that:

`\begin{gathered} P(1,1) \\ Q(3,1) \\ R(1,-2) \\ S(0,0) \end{gathered}`

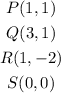
If we sum 1 in the x-coordinate and 4 in the y-coordinate of all points, we would have:

`\begin{gathered} P^(\prime)(2,5) \\ Q^(\prime)(4,5) \\ R^(\prime)(2,2) \\ S^(\prime)(1,4) \end{gathered}`

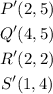
These points are exactly what we have in the second option, so this option is the correct one.