Question

Family A and Family B both have 8 people in their family. The ages of each member is listed below. Which statement is correct about the variability of the two families?Family A: 35,5,42,9,16,3,8,12Family B: 1,5,29,3,7,35,6,9A. The variability is the same for both Family A and Family B because they have the same mean absolute deviation.B. The variability for Family B is greater because the mean absolute deviation is greater for Family B.C. There is not enough information to determine the variability.D. The variability for Family A is greater because the mean absolute deviation is greater for Family A.

Answer 1

Given:

Family A: 35,5,42,9,16,3,8,12

Family B: 1,5,29,3,7,35,6,9

To find the statement which is correct about the variability of the two families:

We know that,

The higher the mean, the higher the variance, and thus the higher the variability.

So, let's find the mean.

Mean for family A is,

`\begin{gathered} Mean=(35+5+42+9+16+3+8+12)/(8) \\ =16.25 \end{gathered}`

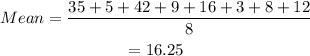
Mean for family B,

`\begin{gathered} \text{Mean}=(1+5+29+3+7+35+6+9)/(8) \\ =11.88 \end{gathered}`

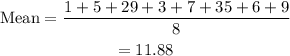
Since the mean value of family A is greater than that of family B.

Since the variability of family A is greater than that of family B.

So, the mean absolute deviation for family A is greater than that for family B.

Therefore, the correct option is D.