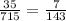Hello!
This is an exercise about combinations. To solve it, we must remember the formula below:
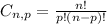
• n,: total of elements
,
• p,: number of elements of the group that we need
Knowing it, let's solve your exercise:
a. In how many ways can four people be selected from this group of thirteen?
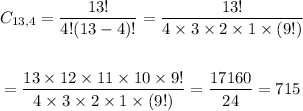
b. In how many ways can four women be selected from the seven women?
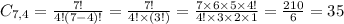
c. Find the probability that the selected group will consist of all women.
4 women, from a total of 7: 35 combinations
(we calculated it in b.)
Total of Combinations: 4 people, from a total of 13: 715 combinations
(we calculated it in a.)
So, we have to write it as a fraction: