ANSWER
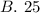
Step-by-step explanation
Let the number of children's tickets be x.
Let the number of adults' tickets be y.
The total number of tickets sold is 62. Therefore, we have that:
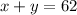
The total amount collected is $365.00. This implies that:
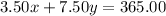
Now, we have two simultaneous equations:
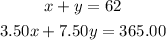
From the first equation, make y the subject of the formula:
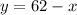
Substitute that into the second equation and solve for x:
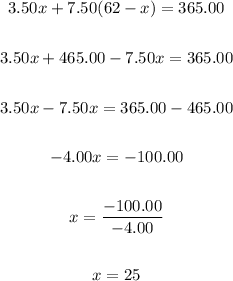
Therefore, 25 children's tickets were sold. The correct answer is option B.