Question

y= -x^2 -14x-20Change from standard form to vertex form based on this quadratic function. I have shown my work on this notepad that I have attached but somewhere in the process I’m still confused because I’m not getting the correct vertex. My vertex should be (-7,29)

Answer 1

y = - (x+7)² + 29

Explanation:

Given the quadratic function:

`y=-x^2-14x-20`

First, complete the square for x:

To do this, divide the coefficient of x by 2, square it and add it to both sides:

`y-49=-x^2-14x+(-49)-20`

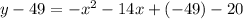
Factor out the negative sign in the first three terms on the right side:

`y-49=-(x^2+14x+49)-20`

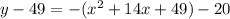
Write the expression in x as a perfect square:

`y-49=-(x+7)^2-20`

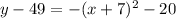
Finally, add 49 to both sides:

`\begin{gathered} y-49+49=-(x+7)^2-20+49 \\ y=-(x+7)^2+29 \end{gathered}`

The vertex form of the quadratic function is:

`y=-(x+7)^2+29`

Note: If you compare the above with the vertex form:

`y=a(x-h)^2+k`

The vertex, (h,k)=(-7, 29).