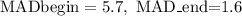For this case we have the following two datasets:
Scores for Essay at Beginning of Teachers' Training
75 78 86 75 89 87 88 77 90 78
Scores for Essay at End of Teachers' Training
79 81 83 80 78 85 81 81 79 83
And we need to calculate the mean Absolute deviation for each case. We need to remember the definition of MAD given by:
![MAD=\frac{\sum ^n_(i\mathop=i)\left|x_i-\operatorname{mean}\right|}{n}]()
And the mean is defined as:
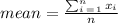
We can calculate the mean for each case and we got:
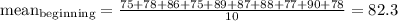
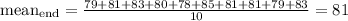
Then finally we can calculate the MAD for each case: