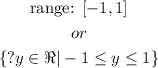We need to find some points, graph, and identify the domain and range for the sine function:
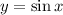
To find some of the points on the graph, we can choose some values of x and then find the respective values of y:

Now, we can plot those points and join them smoothly to obtain the graph:
The graph continues indefinity for infinitely negative and positive values of x. Thus, the domain of this function is:
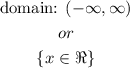
And since y can only have values between -1 and 1 (including -1 and 1), we have: