Given:
The force constant of a spring is k = 100 N/m
The mass of the box is 55 g = 0.055 kg
The maximum compression is

Required:
Speed of the box when it is compressed to x = 7 cm = 0.07 m
Step-by-step explanation:
The speed of the box can be calculated as
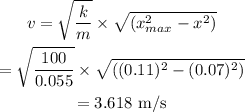
Final Answer: The speed of the box is 3.618 m/s.