The length of the fencing is 500 foot
That means the perimeter of the playground = 500
Assume that the dimensions of it are x and y
So 2x + 2y = 500 ---- perimeter of the rectangular yard
Divide both sides by 2
x + y = 250
Now subtract the two sides by x to find y in terms of x
x - x + y = 250 - x
y = 250 - x --------(1)
Since we need to find the maximum area, let us find the area in terms of x and y
Area of the yard is A
A = xy -------- area the rectangle
Now substitute y by (1)
A= x(250 - x)
A = 250x - x^2
For the maximum area, we will differentiate A with respect to x
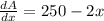
For maximum area equate dA/dx by zero
Since dA/dx = 0
250 - 2x = 0
Add 2x for both sides
250 - 2x + 2x = 0 + 2x
250 = 2x
Divide both sides by 2
125 = x