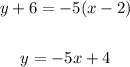Step-by-step explanation
We are given the following:
We are required to determine the equations that have a slope of -5 and passes through (2, -6).
We know that the slope-intercept form of a straight line is given as:
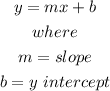
We can determine the given equations as follows:

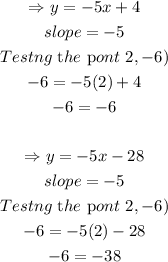
Hence, the answers are: