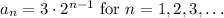Question

Looking for the common ratio to the sequence 3, 6, 12 … is it arithmetic or geometric and lastly the n^th term formula for a( n below ) equals

Answer 1

We have the following sequence: 3,6,12, ...

We can note that the common ratio between consecutive numbers is

`(6)/(3)=(12)/(6)=2`

This implies that the given sequence is a geometric one. Generally, to check whether a given sequence is geometric, we simply checks whether successive entries in the sequence all have the same ratio.

The formula for the n-th term of the sequence is given by

`a_n=a\cdot r^(n-1)`

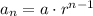
where a is the first term of the sequence and r is the common ratio. From our last results, we have that

`\begin{gathered} a=3 \\ r=2 \end{gathered}`

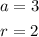
By substituting these result into the above formula, the last term is given as

`a_n=3\cdot2^(n-1)`

Therefore the last term a_n, is given by:

`a_n=3\cdot2^(n-1)\text{ for }n=1,2,3,\ldots`