Question

Find b and c so that y = 20x2 + bx+c has vertex (6, - 2). b= с — > Next Question

Answer 1

We have a quadratic function with unknown parameters b and c and we have to define them in order for the function to have its vertex at (6,-2).

The formula for the x-coordinate of the vertex is:

`x_v=-(b)/(2a)`

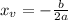
As xv = 6 and a=20, we can find b as:

`\begin{gathered} x_v=-(b)/(2a) \\ 6=(-b)/(2\cdot20) \\ 6\cdot40=-b \\ 240=-b \\ b=-240 \end{gathered}`

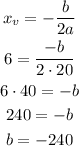
As the y-coordinate of the vertex is:

`y_v=f(x_v)`

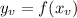
then we can replace with the known information and calculate c as:

`\begin{gathered} y_v=20x^2_v-240x_v+c=-2 \\ 20(6)^2-240\cdot6+c=-2 \\ 20\cdot36-1440+c=-2 \\ 720-1440+c=-2 \\ c=-2+1440-720 \\ c=718 \end{gathered}`

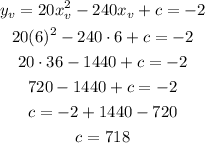
Then, the quadratic equation can be written as:

`y=20x^2-240x+718`

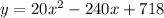
We can check it with a graph: