We have 19 available seats, and 21 reservations.
Of the 21 reservations, 10 are sure, so we have 10 out of the 19 seats that are surely occupied.
Then, we have 9 seats for 11 reservations, each one with 44% chance of being occupied.
We have to calculate the probability that the plane is overbooked. This means that more than 9 of the reservations arrive.
This can be modelled as a binomial distirbution with n = 11 and p = 0.44, representing the 44% chance.
Then, we have to calculate P(x > 9).
This can be calculated as:

and each of the terms can be calculated as:
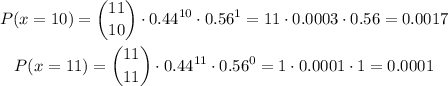
Then:
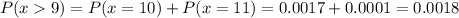
We have a probability of 0.18% of being overbooked (P = 0.0018).
If we want to calculate the probability of having empty seats, we need to calculate P(x<9), meaning that less than 9 of the reservations arrive.
We can express this as:
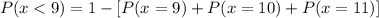
We have to calculate P(x=9) as we already have calculated the other two terms:
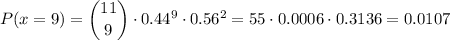
Finally, we can calculate:
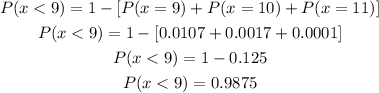
There is a probability of 0.9875 that there is one or more empty seats.
Answer:
There is a probability of 0.0018 of being overbooked.
There is a probability of 0.9875 of having at least one empty seat.