Question

An exponential function f(x) = a · b^× passes through the points (0, 4) and (3, 500). What are the values of a and b?

Answer 1

Given the exponential function:

`f(x)=a\cdot b^x`

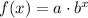
The function passes through the points:

(0, 4) and (3, 500)

Let's find the values of a and b.

Let's use the given points to find a and b.

(0, 4):

Substitute 0 for x, and 4 for f(x), to find the value of a:

`\begin{gathered} f(x)=a\cdot b^x \\ \\ 4=a\cdot b^0 \\ \\ 4=a\cdot1 \\ \\ 4=a \\ \\ a=4 \end{gathered}`

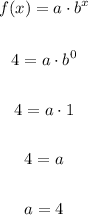
The value of a is 4

(3, 500):

Substitute 3 for x, 500 for f(x) and 4 for a to solve for b:

`\begin{gathered} f(x)=a\cdot b^x \\ \\ 500=4\cdot b^3 \\ \\ \text{Divide both sides by 4:} \\ (500)/(4)=(4\cdot b^3)/(4) \\ \\ 125=b^3 \\ \\ \text{Take the cube root of both sides:} \\ \sqrt[3]{125}=\sqrt[3]{b^3} \\ \\ 5=b \\ \\ b=5 \end{gathered}`

The value of b is 5

ANSWER:

a = 4

b = 5