Question

What is the equation of the line that passes through the point (4,-3) and (2,1)? Show how you found your slope and how you found b write the final equation of the line

Answer 1

The equation of the line is y = -2x+1.

Explanation.

Given:

The straight line passes throught the points (4,-3) and (2,1).

The objective is to find the equation of the line.

Consider the given points as,

`\begin{gathered} (x_1,y_1)=(4,-3) \\ (x_2,y_2)=(2,1) \end{gathered}`

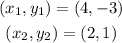
The general equation of straight line is,

`y=mx+b`

Here, m stands for slope of the line and b stands for the yintercept of the line.

The slope of the line can be calculated by the formula,

`m=(y_2-y_1)/(x_2-x_1)`

Substitute the given values in the above formula.

`\begin{gathered} m=(1-(-3))/(2-4) \\ m=(1+3)/(-2) \\ m=(4)/(-2) \\ m=-2 \end{gathered}`

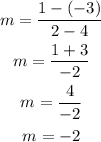
Thus, the slope value is obtained.

Now, the value of b can be calculated by the equation,

`y-y_1=m(x-x_1)`

Substitute the obtained values in the above equation.

`\begin{gathered} y-(-3)=-2(x-2) \\ y+3=-2(x-2) \\ y+3=-2x+4 \\ y=-2x+4-3 \\ y=-2x+1 \end{gathered}`

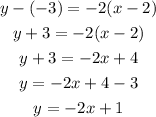
By comparing the above equation with the equation of striaght line y = mx+b,

The value of b can be obtained as, b = +1.

Hence, the required final equation of the line is y = -2x+1.