Question

Answer this question using two different strategies.Your rectangular backyard is to be fenced with 75 m of fencing on three sides (see diagram). What dimensions will yield the most area? Use two different stategies

Answer 1

Step-by-step explanation

From the image, we can see that we have two widths and one length that will make up the fencing of 75m

Therefore, the sum of the dimensions can be expressed as

Strategy 1

`\begin{gathered} 75=2w+l \\ Therefore \\ l=75-2w \end{gathered}`

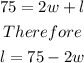
Recall

`\begin{gathered} Area=l* w \\ A=(75-2w)w \\ A=75w-2w^2 \\ A=-2w^2+75w \\ when\text{ we differentiate with respect to w} \\ 0=-4w+75 \\ 4w=75 \\ w=(75)/(4)=18.75m \end{gathered}`

Therefore, the length becomes

`l=75-2(18.75)=37.5m`

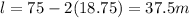
The dimensions are:

Answer: lenght =37.5m

Width=18.75m

Strategy two

`\begin{gathered} From\text{ } \\ A=-2w^2+75w \\ A=-2(w^2-(75w)/(2)) \\ using\text{ the completing the square method} \\ A=-2(w^2-(75)/(2)w+((75)/(4))^2-((75)/(4))^2) \\ A=-2((w-(75)/(4))^2-((75)/(4))^2)) \\ A=-2(w-(75)/(4))^2+2((75^2)/(4^2)) \\ A=-2(w-(75)/(4))^2+(5625)/(8) \end{gathered}`

The vertex form of a quadratic equation is y = a ( x − h )^2 + k, where h is the maximum

`maximum=width=(75)/(4)=18.75m`

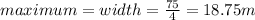
Therefore;

`l=75-2(18.75)=37.5m`

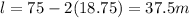
The dimensions are:

Answer: lenght =37.5m

Width=18.75m