Question

Given cos(α)=7/9 and sin(α)<0, calculate the exact value of cot(α).

Answer 1

From the identity

`\sin ^2(\alpha)+\cos ^2(\alpha)=1`

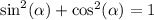
we can find the value for sin(α). Using our value for the cosine and solving the identity for sin(α), we have

`\begin{gathered} \sin ^2(\alpha)+((7)/(9))^2=1 \\ \sin ^2(\alpha)=1-((7)/(9))^2 \\ \sin ^2(\alpha)=1-(7^2)/(9^2) \\ \sin ^2(\alpha)=1-(49)/(81) \\ \sin ^2(\alpha)=(81)/(81)-(49)/(81) \\ \sin ^2(\alpha)=(32)/(81) \\ \sin (\alpha)=\pm_{}\sqrt[]{(32)/(81)} \end{gathered}`

Since sin(α) < 0, we have

`\sin (\alpha)=-_{}\sqrt[]{(32)/(81)}=-\frac{4\sqrt[]{2}}{9}`

The cot(α) is defined as the ratio between the cosine and sine of alpha.

`\cot (\alpha)=(\cos(\alpha))/(\sin(\alpha))`

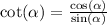
Then, the cot(α) is

`\cot (\alpha)=\frac{(7)/(9)}{-\frac{4\sqrt[]{2}}{9}}=-\frac{7}{4\sqrt[]{2}}=-\frac{7\sqrt[]{2}}{8}`

This is the exact value of cot(α).

`\cot (\alpha)=-\frac{7\sqrt[]{2}}{8}`