Question

The population of the bacteria is initially 20 at the end of week one the population of the bacteria is 30 the population grows by 50% each week what is the bacteria population at the end of week 12. Round to the nearest whole number.

Answer 1

In this case we can use the exponential growth model, given by

`P=P_0(1+r)^t`

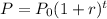
where P_0 is the inital population, r is the rate and t the time. In our case, we have

`\begin{gathered} P_0=20 \\ r=0.5\text{ \lparen corresponding to 50\%\rparen} \\ t=12\text{ week} \end{gathered}`

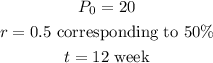
So, by substituting these values into the model, we have

`P=20(1+0.5)^(12)`

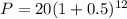
which gives

`\begin{gathered} P=20*129.7463 \\ P=2594.9267 \end{gathered}`

Therefore, by rounding off to the nearest whole number, the answer is 2595 bacteria