Question

A jar contains 6 pennies, 7 nickels and 8 dimes. A child selects 2 coins at random without replacement from the jar. Let X represent the amount in cents of the selected coins.Round your answers to 3 decimal places.Find the probability X = 10. Find the probability X = 11

Answer 1

(a)0.1 (b)0.229

Explanation:

First, briefly recall the following:

• 1 penny = 1 cent

,

• 1 nickel = 5 cents

,

• 1 dime = 10 cents

The child is to select two coins.

There are 6 pennies, 7 nickels and 8 dimes.

The total number of coins = 6 + 7 + 8 = 21.

Let X represent the amount in cents of the selected coins.

(a)X=10

For the child to pick two coins worth 10 cents, the child must pick two nickels.

`\begin{gathered} P(1st\text{ nickel)}=(7)/(21) \\ P(2nd\text{ nickel)}=(6)/(20) \end{gathered}`

Therefore:

`P(X=10)=(7)/(21)*(6)/(20)=0.1`

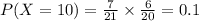
The probability that X=10 is 0.1.

(b)X=11

For the child to pick two coins worth 11 cents, the child must pick 1 dime and 1 penny in any of the two orders below.

• Penny then dime

,

• Dime then penny

`\begin{gathered} P(\text{penny 1st)}* P(\text{dime 2nd)}=(6)/(21)*(8)/(20)=(4)/(35) \\ P(\text{dime 1st)}* P(\text{penny 2nd)}=(8)/(21)*(6)/(20)=(4)/(35) \end{gathered}`

Therefore:

`P(X=11)=(4)/(35)+(4)/(35)=(8)/(35)\approx0.229`

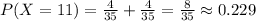
The probability that X=11 is 0.229.