Question

Which similarity statement and postulate or Theorem correctly identity’s the triangles relationship

Answer 1

For two triangles to be similar:

-The corresponding sides must be at the same ratio

-The corresponding angles must be congruent

For the triangles ΔLMN and ΔQPN

We know the length of the two sides.

The corresponding sides are:

LN and QN

MN and PN

If the triangles are similar then:

`(LN)/(QN)=(MN)/(PN)`

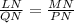
To check if the sides are at the same ratio, you have to calculate the quotient between the corresponding sides:

`(LN)/(QN)=(6)/(8)=(3)/(4)`
`(MN)/(PN)=(9)/(12)=(3)/(4)`

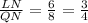
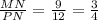
Both pairs of corresponding sides are at the same ratio.

Now, where both triangles meet, the corresponding angles ∠MNL and ∠PNQ are vertically opposite angles, which means that they are equal.

This means that ΔLMN and ΔQPN are similar by SAS Similarity theorem (first option)