To find the length of the string we need to remember that in any right triangle:
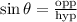
In this case the angle is 48°, the opposite leg is 90 and the hypotenuse will be the length of the string then we have that:
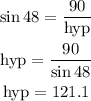
Therefore the length of the string is 121.1 ft