Question

What are the coordinates of the Center and the length of the radius?

Answer 1

Explanation:

Given the equation of the circle below:

`$$x^(2)+y^(2)-4 x-10 y+20=0$$`

We are required to find the coordinates of the center and the length of the radius.

In order to do this, we complete the squares for each of the variables x and y.

First, rearrange the equation:

`x^2-4x+y^2-10y=-20`

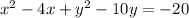
To complete the square for x, divide the coefficient of x by 2, square it and add it to both sides of the equation.

`x^2-4x+\left(-(4)/(2)\right)^2+y^2-10y=-20+\left(-(4)/(2)\right)^2`

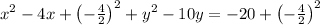
Repeat the same process for y:

`\begin{gathered} x^2-4x+\left(-(4)/(2)\right)^2+y^2-10y+\left(-(10)/(2)\right)^2=-20+\left(-(4)/(2)\right)^2+\left(-(10)/(2)\right)^2 \\ x^2-4x+(-2)^2+y^2-10y+(-5)^2=-20+(-2)^2+(-5)^2 \end{gathered}`

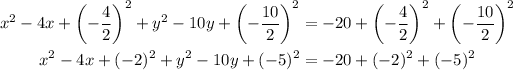
Write the perfect squares and simplify the right-hand side:

`\begin{gathered} (x-2)^2+(y-5)^2=-20+4+25 \\ (x-2)^2+(y-5)^2=9 \end{gathered}`

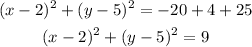
Compare to the standard form of a circle below:

`\begin{gathered} (x-a)^2+(y-b)^2=r^2 \\ \implies(a,b)=(2,5) \\ r^2=9\implies r=3 \end{gathered}`

• The center of the circle = (2, 5)

,

• The length of the radius = 3 units

Option B is correct.