The composite figure is formed by a semicircle and a triangle. To determine its area, you have to calculate the area of both shapes and add them.
1) Area of the semicircle
The area of the semicircle can be calculated as half the area of a circle, following the formula:
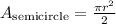
The diameter of the semicircle is 8m, the radius is half the diameter, so r=8/2=4m, replace the length of the diameter on the formula and calculate the area:
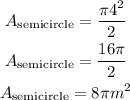
2) Area of the triangle
The area of the triangle can be calculated as half the product of its base and height following the formula:
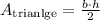
The triangular shape has a base of 8m and a height of 12m, the area can be calculated as follows:
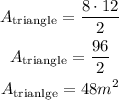
3)Area of the composite figure
Now what's left is to add the calculated areas to determine the area of the composite figure:

The area of the composite figure is 73.12m²