Question

Solve this system of equations byusing the elimination method.6x » 5y = 33x – 8y = –15=72

Answer 1

Given: The system of equations below

`\begin{gathered} equation1:6x-5y=3 \\ equation2:3x-8y=-15 \end{gathered}`

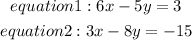
To Determine: The solution of the equations

Solution

Step 1: Eliminate x by multiplying equation 1 by 1 and equation 2 by 2

`\begin{gathered} 1*(6x-5y=3)\rightarrow6x-5y=3 \\ 2*(3x-8y=-15)\rightarrow6x-16y=-30 \end{gathered}`

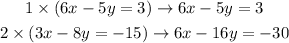
Step 2: Subtract derived equation from equation 2 from the derived equation from equation 1

`\begin{gathered} (6x-5y=3)-(6x-16y=-30) \\ 6x-6x-5y--16y=3--30 \\ -5y+16y=3+30 \\ 11y=33 \\ y=(33)/(11) \\ y=3 \end{gathered}`

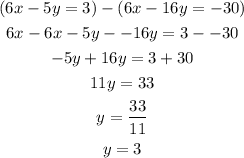
Step 3: Substitute the value of y into equation 1

`\begin{gathered} 6x-5y=3 \\ 6x-5(3)=3 \\ 6x-15=3 \\ 6x=3+15 \\ 6x=18 \\ x=(18)/(6) \\ x=3 \end{gathered}`

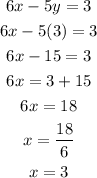
Hence, x = 3, y = 3

(3,3)