Given the distance of 382 miles, and a velocity of 760 miles/hour and a time of 0.583 hour, we can writte the following equation:
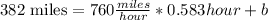
Then the intercept b is:
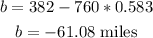
Hence the equation for the first data set is:
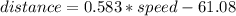
Now the next dataset:
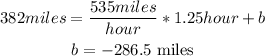
Hence the equation for the second point is:
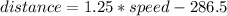
Next, for the third point. By hyperloop, a round trip takes 0.583*2=1.166 hour (go and back), hence in a 12-hour day:
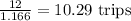
Hence by hyperloop we got 10 trips.
On the other way, by airplane it takes 1.25*2=2.5hour:
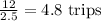
Then by airplane we got 4 round trips.