Step-by-step explanation
We are given the function that defines the profit in relation to the price of the item
The first part of the question:
The form that is most useful for finding the price that gives a profit of 0 dollars will be
the standard form because we can easily substitute p =0 and get the profit
So we have the answer to be
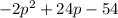
For the second part of the question
The profit, when the price is 0 will be when p =0
so that
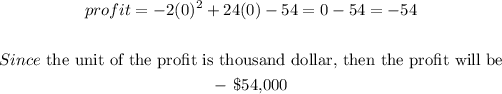
The profit is -$54,000
The third part of the question
The price that gives maximum profit can simply be obtained from the vertex equation
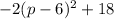
This will be when
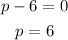
So the price that gives maximum profit is $6