Question

Solve the system state whether the graphs are intersecting, conciding, or parallel. Then classify the system as independent consistent(IC), dependant consistent(DC), or inconsistent(I).

Answer 1

We have the following system of equations:

`\begin{gathered} 5x+2y=6 \\ 10x+4y=12 \end{gathered}`

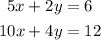
If we multiply the first equation by 2, we have an equivalent system of equations:

`\begin{gathered} 10x+4y=12 \\ 10x+4y=12 \end{gathered}`

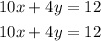
but the equations are the same. This means that the graphs coincide. This also means that the system of equations is dependant consistent. These kind of systems have an infinite number of solutions