Solution:
Let us the line with the equation:
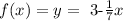
According to this equation, the slope of this line is:
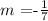
now, the slope of the line perpendicular to the line f(x) would be:
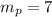
Since the perpendicular line to f(x), passes through the origin, we have that the y-intercept of this line is 0, so the equation of the perpendicular line passing through origin is:
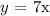
now, to find the intersecting point between the lines, we must equalize both equations of the lines:
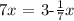
then, solve for x:
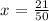
the y-coordinate corresponding to this x, is:
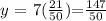
thus, we obtain the point:
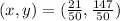
now, the y-intercept of the given line f(x) is when x=0, then:
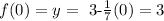
thus, we get the point:
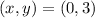
Therefore, we already have the 3 points that define the triangle
so the triangle is bounded by the points
![undefined]()