Question

A large battery is a cylinder with the dimensions shown below. What is the total weight, rounded to the nearest gram, if the density of the battery is ?

Answer 1

Explanation:

Step 1. We have a cylinder with a radius of 4cm and a height of 10cm.

`\begin{gathered} r=4cm \\ h=10cm \end{gathered}`

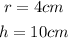
And we also have the density of the cylinder:

`p=12\frac{g\text{ }}{cm^3}`

Step 2. We need to find the weight, which in this case is the mass of the cylinder, using the following formula:

`p=(m)/(V)`

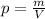
where p is the density, m is the mass, and V is the volume of the cylinder.

Step 3. The volume is:

Substituting the known values and using

`\pi=3.1416`
`V=(3.1416)(4cm)^2(10cm)`

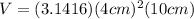
Solving the operations

`V=502.656cm^3`

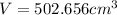
Step 3. Now we go back to our density formula:

`p=(m)/(V)`

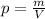
and substitute the known values of the density and the volume:

`12\text{ }g/cm^3=(m)/(502.656cm^3)`

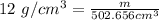
Solving to find the mass:

`\begin{gathered} 12g/cm^3*502.656cm^3=m \\ \downarrow \\ 6,031.872g=m \end{gathered}`

rounding the mass to the nearest gram:

`6,032=m`

The mass in grams is 6,032.

Answer: 6,032