Given:

To Find:
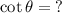
Solution:
Please note that
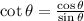
For sin(theta) to be less than zero, then the value is negative. From the knowledge of trigonometry, we can get the third side of the triangle from cos(theta) = 5/8, using the Pythagoras theorem.
From the figure above, h would be calculated using the Pythagoras theorem
![\begin{gathered} 8^2=h^2+5^2 \\ 64=h^2+25 \\ h^2=64-25 \\ h^2=39 \\ h=\sqrt[\square]{39} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/high-school/mo8vjlp921d8vfidkrmlvz1o679x9gnmfb.png)
Therefore;
![\text{sin}\theta=(h)/(8)=\frac{\sqrt[]{39}}{8}](https://img.qammunity.org/2023/formulas/mathematics/high-school/gypahmcf95ihlsd43lv5utd9vlobhaxvu4.png)
Since it is known that sin (theta is negative, then
![\sin \theta=\frac{-\sqrt[]{39}}{8}](https://img.qammunity.org/2023/formulas/mathematics/high-school/v9r97plujxt4fl3m0rjt6prv0vdhklvn3d.png)
Therefore:
![\begin{gathered} \cot \theta=\frac{\cos\theta}{\text{sin}\theta}=(5)/(8)*-\frac{8}{\sqrt[]{39}} \\ \cot \theta=-\frac{5}{\sqrt[]{39}} \\ \text{Rationalize the denominator would give} \\ \cot \theta=\frac{-5*\sqrt[]{39}}{\sqrt[]{39}*\sqrt[]{39}} \\ \cot \theta=\frac{-5\sqrt[]{39}}{39} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/high-school/c3s2jto04mnq8nbfxqypxnt21b9nsqf9mm.png)
Hence, cot (theta) is -5√39/39