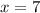If l and m are parallel, this means that the angles I'm going to show you in red must be equal:
So what I'm saying is that:
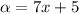
Also, since the angle under alpha and the angle (5x+19) are supplementary:
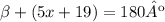
And, as you can see, beta and alpha are supplementary too, so:
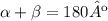
From the second equation we clear beta:
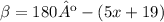
And we replace it in the equation of beta and alpha. Also, we have to replace alpha with the expression in the first equation:
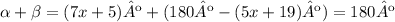
And then, we just clear the x:
I'll take the parenthesis out.
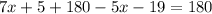
We group the x and add up the constants:
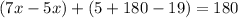
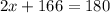
166 goes to the other side as a substraction and the 2 goes dividing:
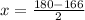
Finally, the value of x is: