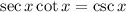We are given the following expression:
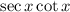
In order to simplify this expression we will use the following relationship:
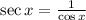
Replacing we get:
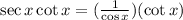
Now we will use the following relationship:
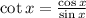
Replacing we get:
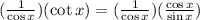
Now we cancel out the cosines of x:
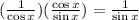
And this expression is equivalent to cosecant of "x", therefore: